penguins-stan-05a

Aufgabe

Wir untersuchen Einflussfaktoren bzw. Prädiktoren auf das Körpergewicht von Pinguinen. In dieser Aufgabe untersuchen wir den Zusammenhang von Schnabellänge (als UV) und Körpergewicht (als AV).

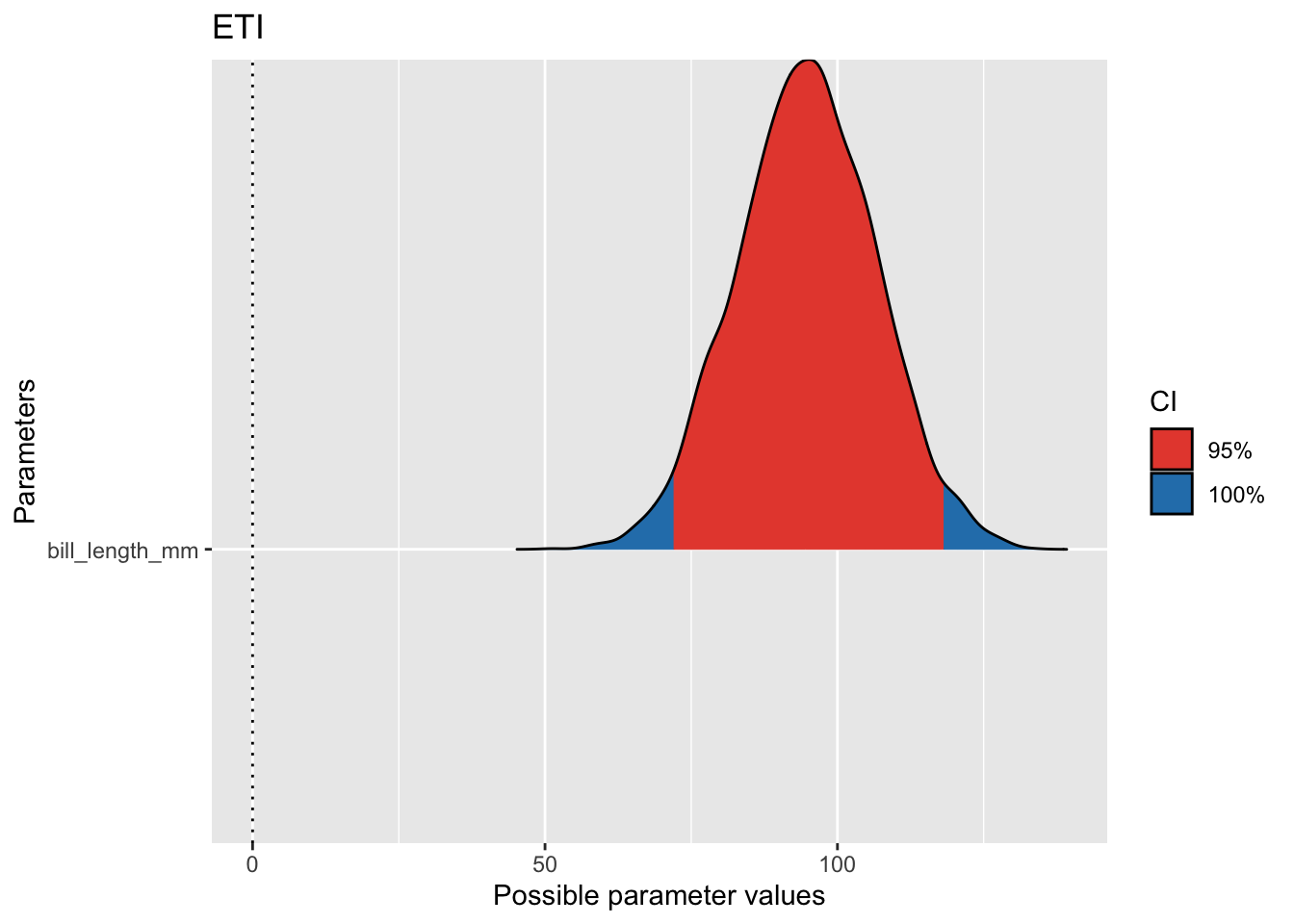
Aufgabe: Wie breit ist das 95%-ETI, wenn Sie nur die Spezies Adelie untersuchen?

Hinweise:

• Sie können den Datensatz z.B. hier beziehen oder über das R-Paket palmerpenguins.
• Weitere Hinweise

Nutzen Sie die folgende Analyse als Grundlage Ihrer Antwort.

Setup:

library(tidyverse)
library(easystats)
library(rstanarm)

data("penguins", package = "palmerpenguins")

Es wird in dieser Aufgabe vorausgesetzt, dass Sie den Datensatz selbständig importieren können. Tipp: Kurzes Googeln hilft ggf., den Datensatz zu finden.

Alternativ könnten Sie den Datensatz als CSV-Datei importieren:

d_path <- "https://vincentarelbundock.github.io/Rdatasets/csv/palmerpenguins/penguins.csv"

Ein Blick in die Daten zur Kontrolle, ob das Importieren richtig funktioniert hat:

penguins <- data_read(d_path)
penguins_adelie <- 
  penguins %>% 
  filter(species == "Adelie")

glimpse(penguins)

Rows: 344
Columns: 9
$ rownames          <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 1…
$ species           <chr> "Adelie", "Adelie", "Adelie", "Adelie", "Adelie", "A…
$ island            <chr> "Torgersen", "Torgersen", "Torgersen", "Torgersen", …
$ bill_length_mm    <dbl> 39.1, 39.5, 40.3, NA, 36.7, 39.3, 38.9, 39.2, 34.1, …
$ bill_depth_mm     <dbl> 18.7, 17.4, 18.0, NA, 19.3, 20.6, 17.8, 19.6, 18.1, …
$ flipper_length_mm <int> 181, 186, 195, NA, 193, 190, 181, 195, 193, 190, 186…
$ body_mass_g       <int> 3750, 3800, 3250, NA, 3450, 3650, 3625, 4675, 3475, …
$ sex               <chr> "male", "female", "female", "", "female", "male", "f…
$ year              <int> 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007…

Vertrauen ist gut, aber – was Golems betrifft – ist Kontrolle eindeutig besser ;-)

m1 <- stan_glm(body_mass_g ~  bill_length_mm,  # Regressionsgleichung
               data = penguins_adelie, #  Daten
               seed = 42,  # Repro.
               refresh = 0)  # nicht so viel Output

parameters(m1, ci = .95, ci_method = "eti")

Parameter	Median	CI	CI_low	CI_high	pd	Rhat	ESS	Prior_Distribution	Prior_Location	Prior_Scale
(Intercept)	22.53919	0.95	-879.18205	913.4400	0.5185	1.000466	3934.802	normal	3700.662	1146.4153
bill_length_mm	94.71685	0.95	71.89291	118.0511	1.0000	1.000492	3910.510	normal	0.000	430.4322

Lösung

Die Lösung lautet also, wie in der Ausgabe zu den Parametern ersichtlich, 46.16.