| Parameter | Median | CI | CI_low | CI_high | pd | Rhat | ESS | Prior_Distribution | Prior_Location | Prior_Scale |
|---|---|---|---|---|---|---|---|---|---|---|
| (Intercept) | 146.1050983 | 0.95 | 145.1605321 | 147.075639 | 1 | 0.9997636 | 4475.401 | normal | 154.5971 | 19.355830 |
| weight_c | 0.9034848 | 0.95 | 0.8201613 | 0.984254 | 1 | 0.9998113 | 4535.592 | normal | 0.0000 | 2.997786 |
Bed-Post-Wskt1
Exercise
Beziehen Sie sich auf das Regressionsmodell, für das die Ausgabe mit stan_glm() hier dargestellt ist:
Betrachten Sie folgende Beziehung (Gleichung bzw. Ungleichung):
Ergänzen Sie das korrekte Zeichen in das Rechteck
Answerlist
Solution
Als Prädiktorwert (X-Variable) wurde der Achsenabschnitt spezifiziert, also
Der vorhergesagte Wert
Für das vorliegende Beispiel heißt das:
Das Ergebnis ist:
(Intercept)
155.11 Im Detail:
Pakete starten:
library(rstanarm)
library(tidyverse)
library(easystats)Daten importieren:
Kung_path <-
"https://raw.githubusercontent.com/sebastiansauer/Lehre/main/data/Howell1a.csv"
d <- read.csv(Kung_path) Daten zentrieren:
d <-
d |> mutate(weight_c = weight - mean(weight))Nur Erwachsene:
d <-
d |>
filter(age >= 18)Modell berechnen:
mod <- stan_glm(height ~ weight_c, data = d, refresh = 0)Paramter des Modells:
parameters(mod)| Parameter | Median | CI | CI_low | CI_high | pd | Rhat | ESS | Prior_Distribution | Prior_Location | Prior_Scale |
|---|---|---|---|---|---|---|---|---|---|---|
| (Intercept) | 146.1050983 | 0.95 | 145.1605321 | 147.075639 | 1 | 0.9997636 | 4475.401 | normal | 154.5971 | 19.355830 |
| weight_c | 0.9034848 | 0.95 | 0.8201613 | 0.984254 | 1 | 0.9998113 | 4535.592 | normal | 0.0000 | 2.997786 |
Modell visualisieren:
estimate_relation(mod) |> plot()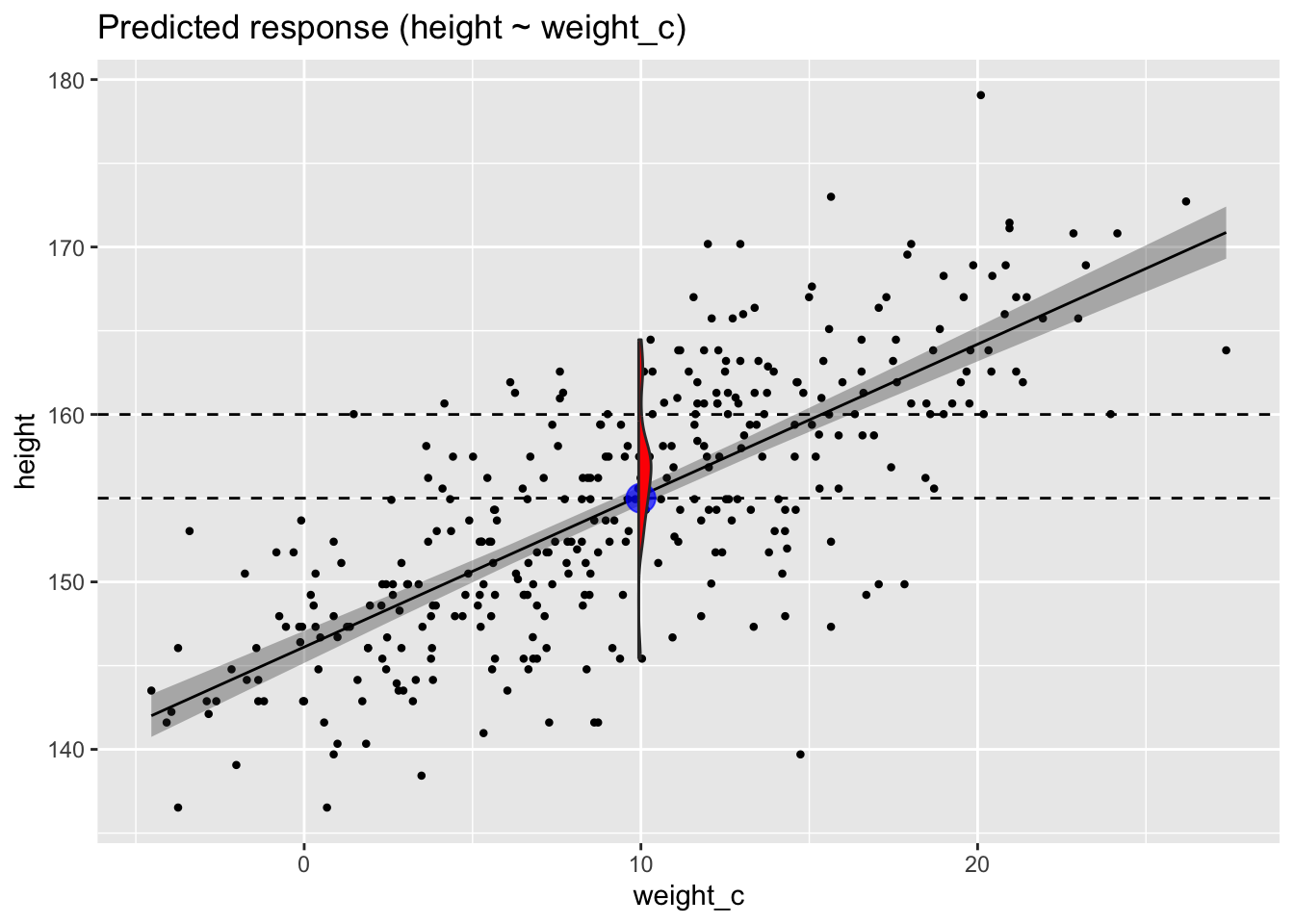
Wie man im Diagramm sieht, ist die Wahrscheinlichkeit bei x = 10 für y=155 größer als für y=160.
Die Wahrscheinlichkeit für einen bestimmten Y-Wert gegeben x = 10` ist auf der Regressionsgeraden am größten (blauer Punkt). Die Punkte auf der Regressionsgeraden sind die vorhergesagten Y-Wert (
Answerlist
- Falsch
- Falsch
- Wahr
- Falsch
- Falsch
Categories:
- regression
- bayes
- post