library(tidyverse)iq08
Aufgabe
An einer Elite-Hochschule wird man nur zugelassen, wenn man sowohl schön als auch schlau ist.
“Schön” sei definiert als eine SD-Einheit über dem mittleren Aussehen, unter der Annahme, dass Aussehen normalverteilt ist.
“Schlau” sei definiert als eine SD-Einheit über dem mittleren Wert, unter der Annahme, dass die Variable normalverteilt ist.
Wie hoch ist die Wahrscheinlichkeit, an dieser Elite-Uni zugelassen zu werden?
Hinweise:
- Nutzen Sie Simulationsmethoden.
- Gehen Sie von folgender Verteilung für Schönheit und für Schlauheit aus: \(X \sim N(0,1)\)
- Intelligenz und Schönheit sollen als unabhängig angenommen werden.
- Geben Sie Anteile oder Wahrscheinlichkeiten stets mit zwei Dezimalstellen an (sofern nicht anders verlangt).
- Simulieren Sie \(n=10^4\) Stichproben.
- Nutzen Sie die Zahl 42 als Startwert für Ihre Zufallszahlen (um die Reproduzierbarkeit zu gewährleisten).
- Weitere Hinweise
Lösung
Die Wahrscheinlichkeit für “schön”, \(S1\) ist gleich der Wahrscheinlichkeit für “Schlau”, \(S2\).
Wir simulieren die Daten:
set.seed(42)
d <- tibble(
id = 1:10^4,
schoenheit = rnorm(n = 10^4, mean = 0, sd = 1),
schlauheit = rnorm(n = 10^4, mean = 0, sd = 1))Da es nur um Anteile (bzw. Wahrscheinlichkeiten) der Population geht, können wir mit z-Werten arbeiten.
Zur Erinnerung: Ein z-Wert von 1 bedeutet, dass der Messwert eine SD-Einheit größer ist als der Mittelwert der Verteilung.
Dann filtern wir wie in der Angabe gefragt:
d2 <-
d %>%
count(schoenheit > 1, schlauheit > 1) %>% # Das Komma wird als logisches UND interpretiert
mutate(prop = n / sum(n))
d2| schoenheit > 1 | schlauheit > 1 | n | prop |
|---|---|---|---|
| FALSE | FALSE | 7082 | 0.7082 |
| FALSE | TRUE | 1364 | 0.1364 |
| TRUE | FALSE | 1314 | 0.1314 |
| TRUE | TRUE | 240 | 0.0240 |
Wieder nehmen wir den Anteil her und bezeichnen ihn als Wahrscheinlichkeit. Das ist eine schöne Sache dieser Simulationsmethoden: Es vereinfacht die Angelegenheit, denn mit Häufigkeiten lässt sich einfacher hantieren als mit Wahrscheinlichkeiten. Und die Anteile erfüllen die Kolmogorov-Axiome, wir können also beruhigt rechnen. Falls Sie also vor Sorge um die Reinheit der Mathematik nicht schlafen konnten, kann ich Sie insofern beruhigen :-)
Natürlich könnte man die Frage auch analytisch lösen (mit dem Multiplikationssatz für unabhängige Ereignisse).
Die Wahrscheinlichkeit für einen Wert \(x >= 115, X \sim N(100,15)\) beträgt:
pr_1sd_ueber_mw <- 1- pnorm(115, 100, 15)
pr_1sd_ueber_mw[1] 0.1586553Dannn:
pr_1sd_ueber_mw * pr_1sd_ueber_mw[1] 0.02517149Antwort: Die Lösung lautet also 0.024.
Interessant ist es vielleicht, die Gesamtpopulation zu visualisieren:
d %>%
mutate(ist_schoen = if_else(schoenheit > 1, TRUE, FALSE),
ist_schlau = if_else(schlauheit > 1, TRUE, FALSE),
ist_schoen_schlau = if_else(ist_schoen & ist_schlau, TRUE, FALSE)) %>%
ggplot() +
aes(x = schoenheit, y = schlauheit, color = ist_schoen_schlau, alpha = .1) +
geom_point()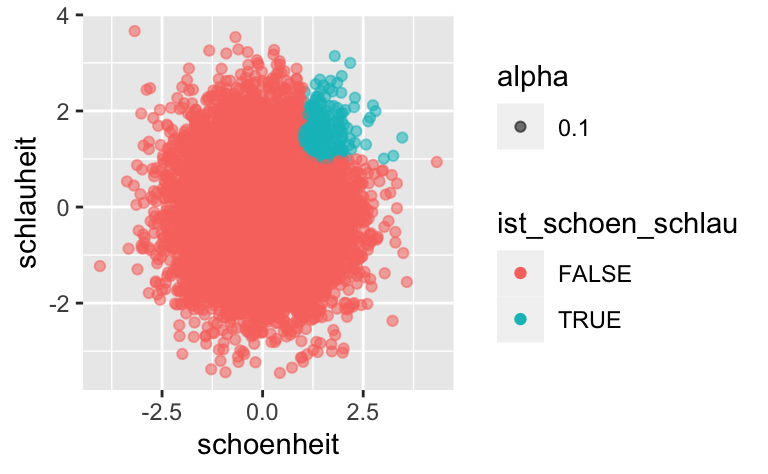
Wäre die Aufnahmeregel, dass es reichte, entweder schön oder schlau (beides ist auch ok) zu sein, wäre der Anteil an zugelassenen Personen größer:
d3 <-
d %>%
count(schoenheit > 1 | schlauheit > 1) %>% # der horizontale Balken steht für das logische ODER.
mutate(prop = n / sum(n))
d3| schoenheit > 1 | schlauheit > 1 | n | prop |
|---|---|---|
| FALSE | 7082 | 0.7082 |
| TRUE | 2918 | 0.2918 |
Categories:
- probability
- simulation
- normal-distribution
- num