adjustieren1a

Aufgabe

Betrachten Sie folgendes Modell, das den Zusammenhang von PS-Zahl und Spritverbrauch untersucht (Datensatz mtcars).

Aber zuerst zentrieren wir den metrischen Prädiktor hp, um den Achsenabschnitt besser interpretieren zu können.

library(tidyverse)
library(easystats)
data(mtcars)

mtcars <-
  mtcars %>% 
  mutate(hp_z = hp - mean(hp))

lm1 <- lm(mpg ~ hp_z, data = mtcars)
parameters(lm1)

Parameter	Coefficient	SE	CI	CI_low	CI_high	t	df_error	p
(Intercept)	20.0906250	0.6828817	0.95	18.6959945	21.4852555	29.420359	30	0e+00
hp_z	-0.0682283	0.0101193	0.95	-0.0888947	-0.0475619	-6.742388	30	2e-07

Jetzt können wir aus dem Achsenabschnitt (Intercept) herauslesen, dass ein Auto mit hp_z = 0 - also mit mittlerer PS-Zahl - vielleicht gut 20 Meilen weit mit einer Gallone Sprit kommt.

Zur Verdeutlichung ein Diagramm zum Modell:

estimate_relation(lm1) |> plot()

Adjustieren Sie im Modell die PS-Zahl um die Art des Schaltgetriebes (am), so dass das neue Modell den statistischen Effekt (nicht notwendig auch kausal) der PS-Zahl bereinigt bzw. unabhängig von der Art des Schaltgetriebes widerspiegelt!

Geben Sie den Punktschätzer für den Effekt von am in diesem Modell an!

Hinweise:

• am=0 ist ein Auto mit Automatikgetriebe.
• Wir gehen davon aus, dass der Regressionseffekt gleich stark ist auf allen (beiden) Stufen von am. M.a.W.: Es liegt kein Interaktionseffekt vor.
• Beachten Sie die üblichen Hinweise des Datenwerks.
• Nutzen Sie lm, um das Modell zu berechnen.

Lösung

lm2 <- lm(mpg ~ hp_z + am, data = mtcars)
parameters(lm2)

Parameter	Coefficient	SE	CI	CI_low	CI_high	t	df_error	p
(Intercept)	17.9468091	0.6758845	0.95	16.5644701	19.329148	26.553072	29	0.00e+00
hp_z	-0.0588878	0.0078567	0.95	-0.0749567	-0.042819	-7.495191	29	0.00e+00
am	5.2770853	1.0795406	0.95	3.0691769	7.484994	4.888269	29	3.46e-05

Die Spalte Coefficient gibt den mittleren geschätzten Wert für den jeweiligen Koeffizienten an, also den Schätzwert zum Koeffizienten.

Die Koeffizienten zeigen, dass der Achsenabschnitt für Autos mit Automatikgetriebe um etwa 5 Meilen geringer ist als für Autos mit manueller Schaltung: Ein durchschnittliches Auto mit manueller Schaltung kommt also etwa 5 Meilen weiter als ein Auto mit Automatikschaltung, glaubt unser Modell.

estimate_relation(lm2) |> plot()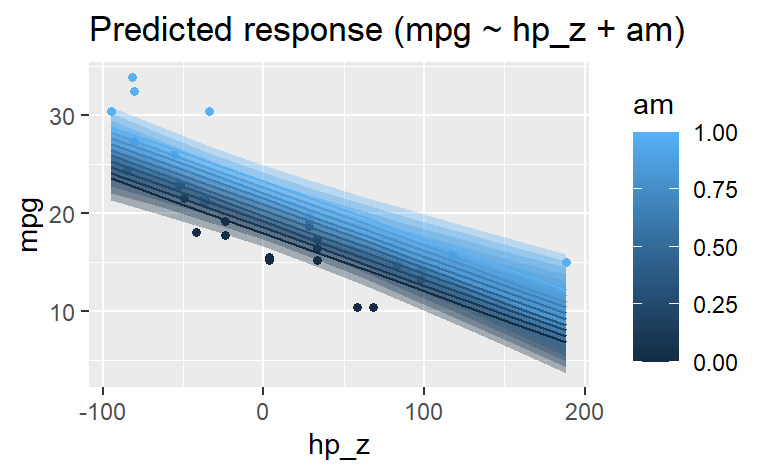

am wird als numerische Variable erkannt. Das ist nicht sinnvoll, da am eher eine kategoriale Variable ist.

Das können wir so ändern:

mtcars <- 
  mtcars |> 
  mutate(am = factor(am))

lm3 <- lm(mpg ~ hp_z + am, data = mtcars)
parameters(lm3)

Parameter	Coefficient	SE	CI	CI_low	CI_high	t	df_error	p
(Intercept)	17.9468091	0.6758845	0.95	16.5644701	19.329148	26.553072	29	0.00e+00
hp_z	-0.0588878	0.0078567	0.95	-0.0749567	-0.042819	-7.495191	29	0.00e+00
am1	5.2770853	1.0795406	0.95	3.0691769	7.484994	4.888269	29	3.46e-05

Die Koeffizienten bleiben gleich.

Lösung: 5.28.

Aber im Diagramm wird am jetzt als Faktor-Variable erkannt, was Sinn macht:

estimate_relation(lm3) |> plot()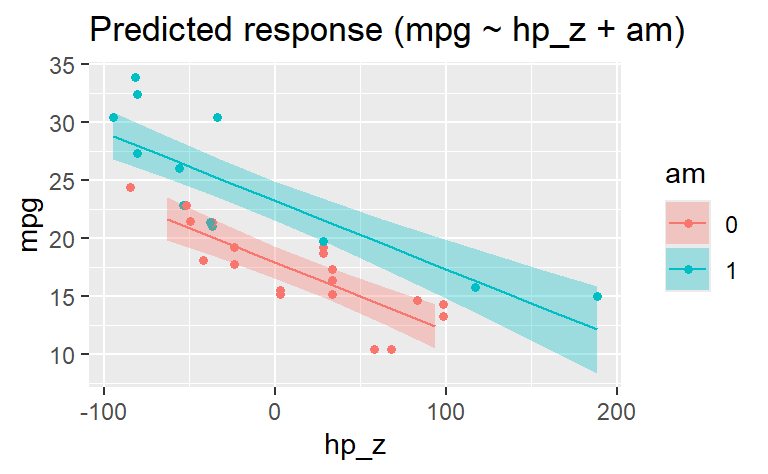

Man könnte hier noch einen Interaktionseffekt ergänzen.

---

Categories:

• regression
• ‘2023’
• string