penguins-stan-04a

bayes
regression
Published

December 10, 2024

Aufgabe

Wir untersuchen Einflussfaktoren bzw. Prädiktoren auf das Körpergewicht von Pinguinen. In dieser Aufgabe untersuchen wir den Zusammenhang von Schnabellänge (als UV) und Körpergewicht (als AV).

Aufgabe:

Wie groß ist die Wahrscheinlichkeit, dass der Effekt vorhanden ist (also größer als Null ist), die “Effektwahrscheinlichkeit”? Geben Sie die Wahrscheinlichkeit an.

Hinweise:

  • Nutzen Sie den Datensatz zu den Palmer Penguins.
  • Verwenden Sie Methoden der Bayes-Statistik und die Software Stan.
  • Sie können den Datensatz z.B. hier beziehen oder über das R-Paket palmerpenguins.
  • Weitere Hinweise

Setup:

library(tidyverse)
library(easystats)
library(rstanarm)

data("penguins", package = "palmerpenguins")

Es wird in dieser Aufgabe vorausgesetzt, dass Sie den Datensatz selbständig importieren können. Tipp: Kurzes Googeln hilft ggf., den Datensatz zu finden.

Alternativ könnten Sie den Datensatz als CSV-Datei importieren:

d_path <- "https://vincentarelbundock.github.io/Rdatasets/csv/palmerpenguins/penguins.csv"
penguins <- data_read(d_path)

Ein Blick in die Daten zur Kontrolle, ob das Importieren richtig funktioniert hat:

glimpse(penguins)
Rows: 344
Columns: 8
$ species           <fct> Adelie, Adelie, Adelie, Adelie, Adelie, Adelie, Adel…
$ island            <fct> Torgersen, Torgersen, Torgersen, Torgersen, Torgerse…
$ bill_length_mm    <dbl> 39.1, 39.5, 40.3, NA, 36.7, 39.3, 38.9, 39.2, 34.1, …
$ bill_depth_mm     <dbl> 18.7, 17.4, 18.0, NA, 19.3, 20.6, 17.8, 19.6, 18.1, …
$ flipper_length_mm <int> 181, 186, 195, NA, 193, 190, 181, 195, 193, 190, 186…
$ body_mass_g       <int> 3750, 3800, 3250, NA, 3450, 3650, 3625, 4675, 3475, …
$ sex               <fct> male, female, female, NA, female, male, female, male…
$ year              <int> 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007…

Vertrauen ist gut, aber - was Golems betrifft - ist Kontrolle eindeutig besser ;-)

m1 <- stan_glm(body_mass_g ~  bill_length_mm,  # Regressionsgleichung
               data = penguins, #  Daten
               seed = 42,  # Repro.
               refresh = 0)  # nicht so viel Output
parameters(m1)
Parameter Median CI CI_low CI_high pd Rhat ESS Prior_Distribution Prior_Location Prior_Scale
(Intercept) 359.9393 0.95 -210.59190 927.8249 0.89575 1.000485 4117.553 normal 4201.754 2004.8863
bill_length_mm 87.4472 0.95 74.55696 100.2532 1.00000 1.000491 4123.761 normal 0.000 367.2233

ETI:

eti(m1) |> plot()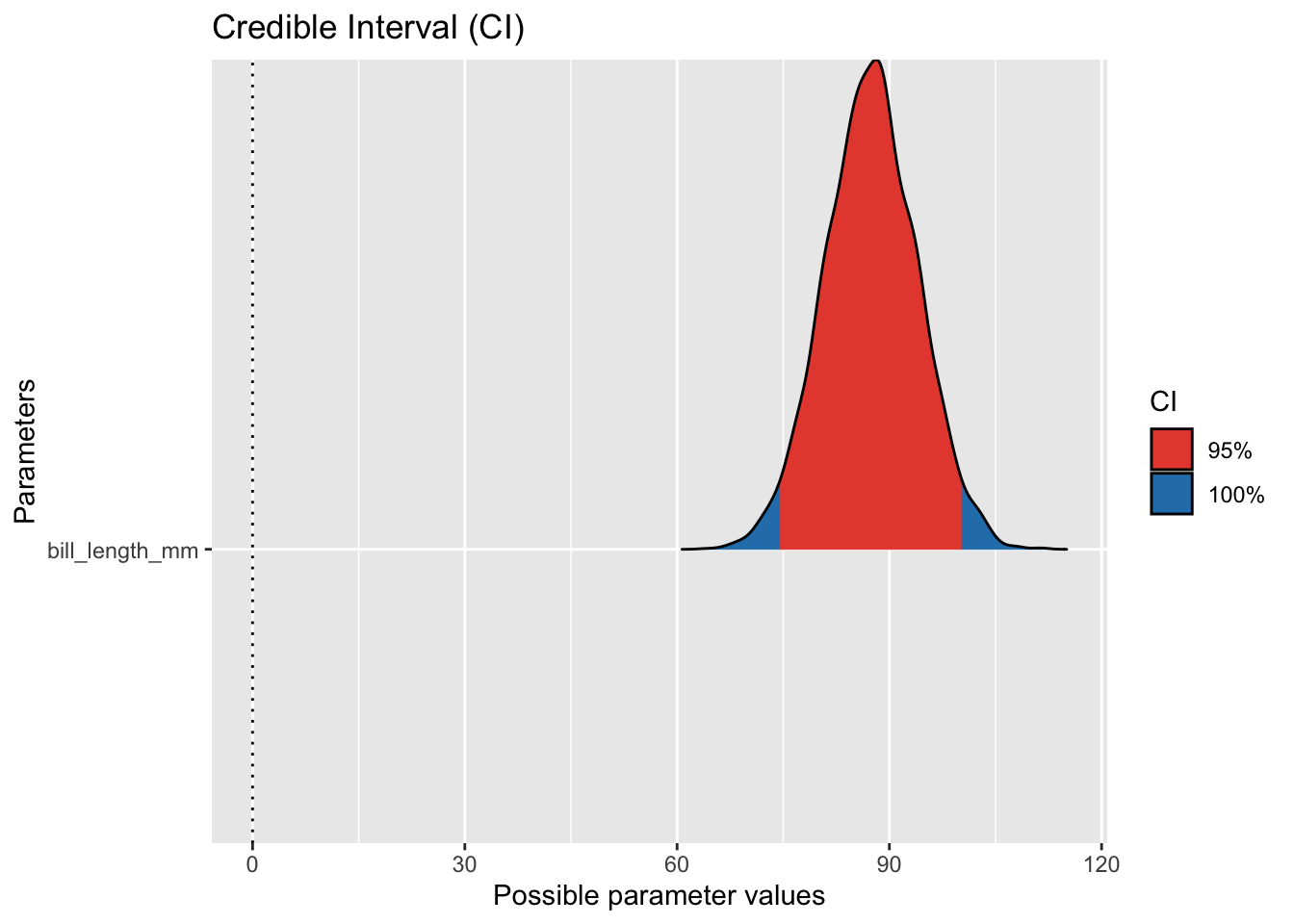











Lösung

Man sieht im Diagramm direkt, dass 100% des Schätzbereichs rechts von der Null ist. Daher ist die Effektwahrscheinlichkeit 100%.

Alternativ bekommt man die Statistik auch mit parameters(), wie in der Tabelle oben in der Spalte pd ersichtlich.

Mit pd() kann man sich die Effektwahrscheinlichkeit (“probability of direction”) ausgeben lassen:

pd(m1)
Parameter pd Effects Component
(Intercept) 0.89575 fixed conditional
bill_length_mm 1.00000 fixed conditional

Mehr Informationen zu dieser Statistik findet sich hier oder hier.

Die Lösung lautet also 1.

Categories:

  • bayes
  • regression
  • exam-22